How Much Data Do You Really Need?
Written by Gal Hyams, Dan Malowany, Ariel Biller, and Gregory Axler
Deep learning models are notorious for their endless appetite for training data. The process of acquiring high-quality annotated data consumes many types of resources — mostly cash. The growing amounts of data as the machine learning projects progress, lead to other undesired consequences, such as slowing down all of R&D. Therefore, veteran project leaders always look at the overall performance gains brought upon by additional increments of their dataset. More often than not, especially if the new data is relatively similar to the existing one, one will encounter the phenomena of Diminishing Returns.
The law of diminishing returns states that when you continuously add more and more input in a productive process, it will actually yield progressively smaller increases in output. This phenomena was mentioned by 18th century economist such as Turgot and Adam Smith and articulated in 1815 by the British economist David Ricardo. When addressing the influence of training data volume on model performance, the law of diminishing returns suggests that each increment in train set size will tend to contribute less to the predetermined success metrics.
When a project leader is able to monitor, and even quantify, the diminishing returns effect in their machine learning project, they are able to attain finer degrees of control throughout its lifetime. For example: estimating how much data is required to reach the project goal; avoiding redundant training sessions; or even predicting whether the current model architecture will be able to achieve the target metric. This knowledge effectively provides a tool for optimal management of time, manpower, and computing resources.
Monitoring Diminishing Returns in Object Detection
Does the reality of diminishing returns also apply to object detection tasks? We decided to explore the answer to this question by training detectors on incremental fractions of two representative datasets: (1) Common Objects in Context (COCO) and (2) Berkeley Deep Drive (BDD). The evaluation of each model was made by looking at the corresponding validation set. Data preparation was done using this script and the metadata subsets are available here. The COCO dataset contains 80 object categories, some of which are scarce. When sampling subsets of this dataset, the rare categories are strongly underrepresented, some things do not even appear at all.
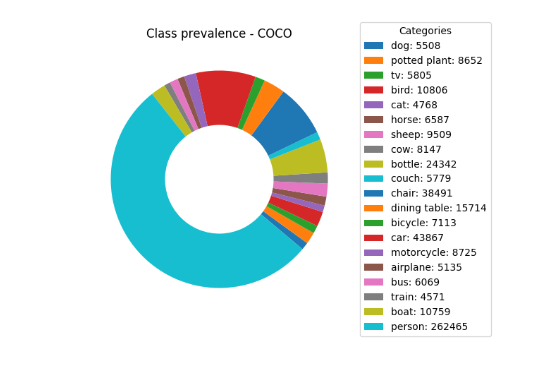
Therefore, we trained and evaluated the model only on the twenty labels appearing on the Visual Object Classes (VOC) dataset. These categories are some of the most common in COCO and are relatively free of mislabeling. The resulted class prevalence and sample collage of labeled images from COCO training set are presented in the figure below.

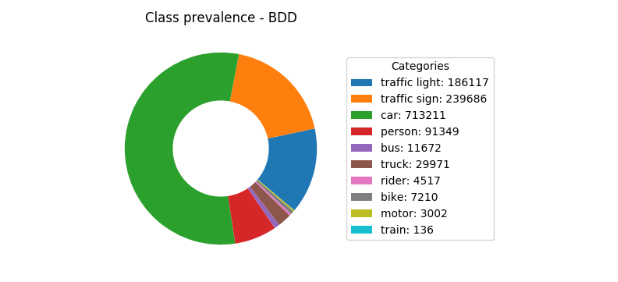
On the BDD dataset, the stuff categories, ‘drivable area’ and ‘lane’, which have an amorphous spatial extent or shape, were ignored. The category ‘rider’ was mapped to the ‘person’ category. The class prevalence and labeled image collage sample of the BDD training set can be seen in figure 2.

The Single Shot Detector (SSD) meta-architecture was used with two popular backbones: MobileNet-v2 and ResNet101. Training was done on the training set’s samples. The results were evaluated by the respective validation sets of each dataset. To emulate the common case of transfer learning, the two models are pre-trained on the open images dataset (v4) as found in TensorFlow’s detection model zoo. The MobileNet-based model was trained using RMSProp for 200,000 training steps of batch size of 12. The models with ResNet-101 backbone were trained for 300,000 training steps of batch size of 4 via momentum optimizer.
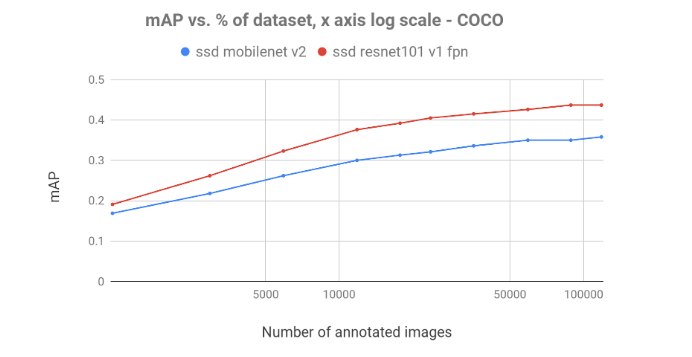
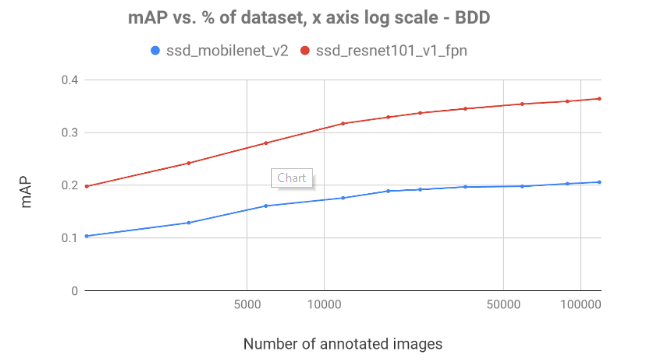
In figure 3, we can see the mAP achieved by the models:
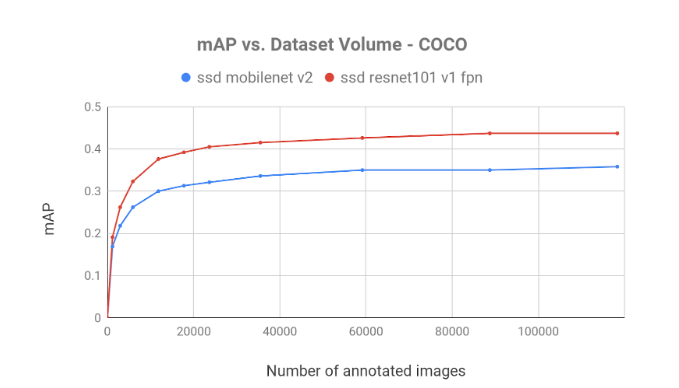
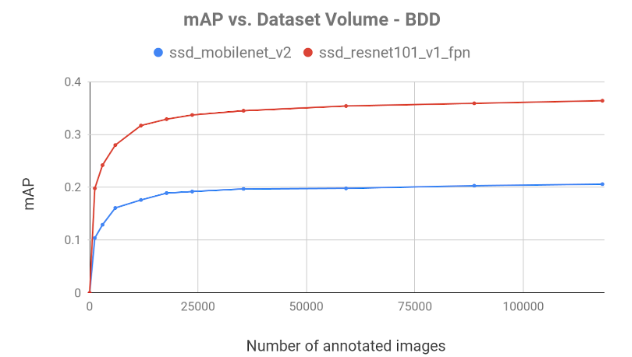
Figure 3, shows the slow growth of mAP, demonstrating the diminishing returns of additional annotated frames. On both datasets with both models, we observe a rapid increase in mAP which decreases as the data volume expands. Common sense suggests that the diminishing returns effect occurs in most datasets and models.
Predicting Diminishing Returns
The ability to predict the diminishing returns effect is a valuable addition to any deep-learning manager’s toolbox. It enables better-informed decisions throughout the lifecycle of the project, saving on valuable resources. Generally, the diminishing returns of each project depends on the data complexity and model architecture; however, as demonstrated above, the diminishing returns effect can act similarly across different tasks.
Indeed, diminishing returns modeling is widespread. The problem is that prevalent modeling of diminishing returns are a-posteriori — they fit to the observed data, but poorly predict the escalation of the diminishing returns dynamics.
Consider the classic model for describing diminishing returns dynamics – the Asymptotic Regression Model (ARM):
f(x) =a1–a2*et*a3
When t is the dataset volume, and ai are learned parameters. This asymptotic model fits well to the diminishing returns curve, when supplied with all the empirical data. Notwithstanding, when predicting the mAP evolution, the ARM struggled to predict the late experiments that mAP based on the smaller scale experiments. The learned model just could not place its asymptotic line properly when it is not given. Clearly this is because in this model, the asymptotic line is directly described by the parameter a1. Generally, when a function’s asymptotic line is not known, it is very difficult to predict its trend.
To overcome this problem, we chose a non-asymptotic Logarithmic regression model:
f(x)=x・log(a1) +a2
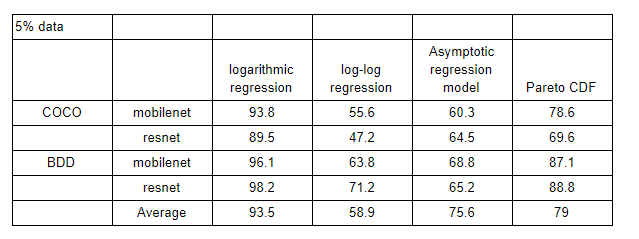
This function predicted the ongoing mAP curve well, as can be seen on figure 5 and table 1 and proved to be a fairly useful empirical tool. This model both practically approximates an asymptotic model and predicts the diminishing returns dynamics based on a few early experiments. Nonetheless, performing a log transformation (figures 4) reveals that the mAP escalation starts as a logarithmic function, and as the data volume expands this increase becomes sub-logarithmic. Therefore, the logarithmic regression may be an efficient tool for diminishing returns prediction, but its accuracy is limited. Interestingly, previous mentions of the data volume’s diminishing returns in deep learning projects is described as logarithmic or sub logarithmic.
The log-log regression, i.e f=x・log(log(t)) + a, despite representing a closer approximation to an asymptotic model, was not as successful in the prediction task (table 1). Though the logarithmic regression fits relatively well to our diminishing returns empirical data, the Pareto CDF might actually yield preferable predictions under scarcity of observation. When predicting diminishing returns, the available empirical data (set volume, resulting mAP) is usually scarce due to the costs involved in obtaining them. This often leads to an overfit of the predictor parameters. The Pareto CDF, containing only a single learnable parameter, is as resilient to this phenomena as a model can get:
f(x)=1 – (1/t)x
Unfortunately, a single-parameter function, besides being characterized by overfitting resilience, is too rigid. Indeed, as described in table 1, the Pareto CDF does not provide as accurate predictions as the logarithmic-regression does.
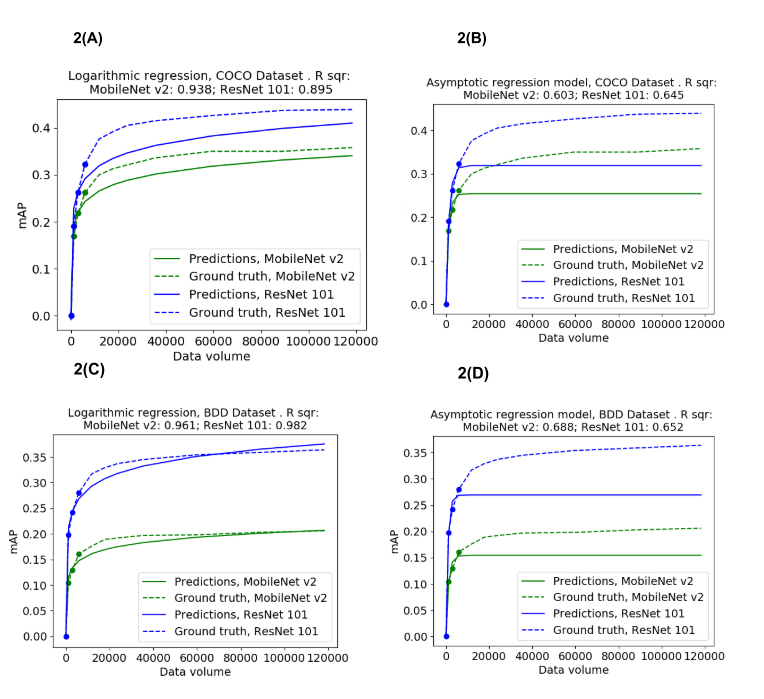
Table 1: Prediction of diminishing returns dynamics: a survey of the various models, given only 5% of the dataset.
Conclusion
It is clear from the experiments above that the law of diminishing returns applies to and can have a detrimental effect to any deep learning project. However, its unavoidable presence may also be exploited as a predictive tool. At the very least, monitoring its effect provides a way to assess how much data is needed for the different stages of the project lifecycle, from hyperparameter search to model fine tuning. Ultimately, it is clear that prior knowledge of the expected final model performance can help with any architecture search efforts. Predicting the diminishing returns of your project will help save a substantial amount of time & money.
The above research was done using trains, our open-source experiments manager for deep learning computer vision — making it easy to craft datasets, clone experiments over different datasets and models, and continuously monitor and compare experiments results.
You are welcome to predict your project’s diminishing returns and even design and evaluate new diminishing returns models using this Jupyter Notebook.
In our next blog, we will explore biased datasets where class imbalance is prominent. We will examine the methods that deal with this common malady: dataset de-biasing, specialized losses (can anyone say focal?) and even complementary synthetic data. So stay tuned and follow us!